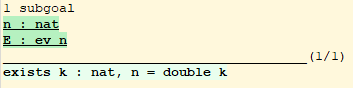\[\begin{split}\newcommand{\as}{\kw{as}} \newcommand{\case}{\kw{case}} \newcommand{\cons}{\textsf{cons}} \newcommand{\consf}{\textsf{consf}} \newcommand{\emptyf}{\textsf{emptyf}} \newcommand{\End}{\kw{End}} \newcommand{\kwend}{\kw{end}} \newcommand{\even}{\textsf{even}} \newcommand{\evenO}{\textsf{even}_\textsf{O}} \newcommand{\evenS}{\textsf{even}_\textsf{S}} \newcommand{\Fix}{\kw{Fix}} \newcommand{\fix}{\kw{fix}} \newcommand{\for}{\textsf{for}} \newcommand{\forest}{\textsf{forest}} \newcommand{\Functor}{\kw{Functor}} \newcommand{\In}{\kw{in}} \newcommand{\ind}[3]{\kw{Ind}~[#1]\left(#2\mathrm{~:=~}#3\right)} \newcommand{\Indp}[4]{\kw{Ind}_{#4}[#1](#2:=#3)} \newcommand{\Indpstr}[5]{\kw{Ind}_{#4}[#1](#2:=#3)/{#5}} \newcommand{\injective}{\kw{injective}} \newcommand{\kw}[1]{\textsf{#1}} \newcommand{\length}{\textsf{length}} \newcommand{\letin}[3]{\kw{let}~#1:=#2~\kw{in}~#3} \newcommand{\List}{\textsf{list}} \newcommand{\lra}{\longrightarrow} \newcommand{\Match}{\kw{match}} \newcommand{\Mod}[3]{{\kw{Mod}}({#1}:{#2}\,\zeroone{:={#3}})} \newcommand{\ModImp}[3]{{\kw{Mod}}({#1}:{#2}:={#3})} \newcommand{\ModA}[2]{{\kw{ModA}}({#1}=={#2})} \newcommand{\ModS}[2]{{\kw{Mod}}({#1}:{#2})} \newcommand{\ModType}[2]{{\kw{ModType}}({#1}:={#2})} \newcommand{\mto}{.\;} \newcommand{\nat}{\textsf{nat}} \newcommand{\Nil}{\textsf{nil}} \newcommand{\nilhl}{\textsf{nil\_hl}} \newcommand{\nO}{\textsf{O}} \newcommand{\node}{\textsf{node}} \newcommand{\nS}{\textsf{S}} \newcommand{\odd}{\textsf{odd}} \newcommand{\oddS}{\textsf{odd}_\textsf{S}} \newcommand{\ovl}[1]{\overline{#1}} \newcommand{\Pair}{\textsf{pair}} \newcommand{\plus}{\mathsf{plus}} \newcommand{\SProp}{\textsf{SProp}} \newcommand{\Prop}{\textsf{Prop}} \newcommand{\return}{\kw{return}} \newcommand{\Set}{\textsf{Set}} \newcommand{\Sort}{\mathcal{S}} \newcommand{\Str}{\textsf{Stream}} \newcommand{\Struct}{\kw{Struct}} \newcommand{\subst}[3]{#1\{#2/#3\}} \newcommand{\tl}{\textsf{tl}} \newcommand{\tree}{\textsf{tree}} \newcommand{\trii}{\triangleright_\iota} \newcommand{\Type}{\textsf{Type}} \newcommand{\WEV}[3]{\mbox{$#1[] \vdash #2 \lra #3$}} \newcommand{\WEVT}[3]{\mbox{$#1[] \vdash #2 \lra$}\\ \mbox{$ #3$}} \newcommand{\WF}[2]{{\mathcal{W\!F}}(#1)[#2]} \newcommand{\WFE}[1]{\WF{E}{#1}} \newcommand{\WFT}[2]{#1[] \vdash {\mathcal{W\!F}}(#2)} \newcommand{\WFTWOLINES}[2]{{\mathcal{W\!F}}\begin{array}{l}(#1)\\\mbox{}[{#2}]\end{array}} \newcommand{\with}{\kw{with}} \newcommand{\WS}[3]{#1[] \vdash #2 <: #3} \newcommand{\WSE}[2]{\WS{E}{#1}{#2}} \newcommand{\WT}[4]{#1[#2] \vdash #3 : #4} \newcommand{\WTE}[3]{\WT{E}{#1}{#2}{#3}} \newcommand{\WTEG}[2]{\WTE{\Gamma}{#1}{#2}} \newcommand{\WTM}[3]{\WT{#1}{}{#2}{#3}} \newcommand{\zeroone}[1]{[{#1}]} \end{split}\]

Proof mode¶

Proof mode is used to prove theorems. Coq enters proof mode when you begin a proof, such as with the Theorem command. It exits proof mode when you complete a proof, such as with the Qed command. Tactics, which are available only in proof mode, incrementally transform incomplete proofs to eventually generate a complete proof.

When you run Coq interactively, such as through CoqIDE, Proof General or coqtop, Coq shows the current proof state (the incomplete proof) as you enter tactics. This information isn't shown when you run Coq in batch mode with coqc.

Proof State¶

The proof state consists of one or more unproven goals. Each goal has a conclusion (the statement that is to be proven) and a local context, which contains named hypotheses (which are propositions), variables and local definitions that can be used in proving the conclusion. The proof may also use constants from the global environment such as definitions and proven theorems.

(Note that conclusion is also used to refer to the last part of an implication. For example, in A -> B -> C, A and B are premises and C is the conclusion.)

The term "goal" may refer to an entire goal or to the conclusion of a goal, depending on the context.

The conclusion appears below a line and the local context appears above the line. The conclusion is a type. Each item in the local context begins with a name and ends, after a colon, with an associated type. Local definitions are shown in the form n := 0 : nat, for example, in which nat is the type of 0.

The local context of a goal contains items specific to the goal as well as section-local variables and hypotheses (see Assumptions) defined in the current section. The latter are included in the initial proof state. Items in the local context are ordered; an item can only refer to items that appear before it. (A more mathematical description of the local context is here.)

The global environment has definitions and proven theorems that are global in scope. (A more mathematical description of the global environment is here.)

When you begin proving a theorem, the proof state shows the statement of the theorem below the line and often nothing in the local context:

Parameter P: nat -> Prop.: P is declared

Goal forall n m: nat, n > m -> P 1 /\ P 2.: 1 goal ============================ forall n m : nat, n > m -> P 1 /\ P 2

After applying the intros tactic, we see hypotheses above the line. The names of variables (n and m) and hypotheses (H) appear before a colon, followed by their type. The type doesn't have to be a provable statement. For example, 0 = 1 and False are both valid and useful types.

intros.: 1 goal n, m : nat H : n > m ============================ P 1 /\ P 2

Some tactics, such as split, create new goals, which may be referred to as subgoals for clarity. Goals are numbered from 1 to N at each step of the proof to permit applying a tactic to specific goals. The local context is only shown for the first goal.

split.: 2 goals n, m : nat H : n > m ============================ P 1 goal 2 is: P 2

"Variables" may refer specifically to local context items introduced from forall variables for which the type of their type is Set or Type. "Hypotheses" refers to items that are propositions, for which the type of their type is Prop or SProp, but these terms are also used interchangeably.

let t_n := type of n in idtac "type of n :" t_n; let tt_n := type of t_n in idtac "type of" t_n ":" tt_n.: type of n : nat type of nat : Set
let t_H := type of H in idtac "type of H :" t_H; let tt_H := type of t_H in idtac "type of" t_H ":" tt_H.: type of H : (n > m) type of (n > m) : Prop

A proof script, consisting of the tactics that are applied to prove a theorem, is often informally referred to as a "proof". The real proof, whether complete or incomplete, is the associated term, the proof term, which users may occasionally want to examine. (This is based on the Curry-Howard isomorphism [How80][Bar81][GLT89][Hue89], which is a correspondence between between proofs and terms and between propositions and types of λ-calculus. The isomorphism is also sometimes called the "propositions-as-types correspondence".)

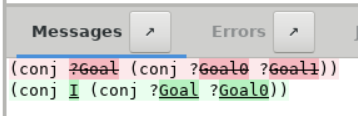
The Show Proof command displays the incomplete proof term before you've completed the proof. For example, here's the proof term after using the split tactic above:

Show Proof.: (fun (n m : nat) (H : n > m) => conj ?Goal ?Goal0)

The incomplete parts, the goals, are represented by existential variables with names that begin with ?Goal. (Note that some existential variables are not goals.) The Show Existentials command shows each existential with the hypotheses and conclusion for the associated goal.

Show Existentials.: Existential 1 = ?Goal : [n : nat m : nat H : n > m |- P 1] Existential 2 = ?Goal0 : [n : nat m : nat H : n > m |- P 2]

Users can control which goals are displayed in the context by focusing goals. Focusing lets the user (initially) pick a single goal to work on. Focusing operations can be nested.

Tactics such as eapply create existential variables as placeholders for undetermined variables that become shelved goals. Shelved goals are not shown in the context by default, but they can be unshelved to make them visible. Other tactics may automatically resolve these goals (whether shelved or not); the purpose of shelving is to hide goals that the user usually doesn't need to think about. See Existential variables and this example.

Coq's kernel verifies the correctness of proof terms when it exits proof mode by checking that the proof term is well-typed and that its type is the same as the theorem statement.

After a proof is completed, Print <theorem_name> shows the proof term and its type. The type appears after the colon (forall ...), as for this theorem from Coq's standard library:

Print proj1.: Fetching opaque proofs from disk for Coq.Init.Logic proj1 = fun (A B : Prop) (H : A /\ B) => match H with | conj x x0 => (fun (H0 : A) (_ : B) => H0) x x0 end : forall A B : Prop, A /\ B -> A Arguments proj1 [A B]%type_scope _

Note

Many tactics accept terms as arguments and frequently refer to them with wording such as "the type of term". When term is the name of a theorem or lemma, this wording refers to the type of the proof term, which is what's given in the Theorem statement. When term is the name of a hypothesis, the wording refers to the type shown in the context for the hypothesis (i.e., after the colon). For terms that are more complex than just an ident, you can use Check term to display their type.

Entering and exiting proof mode¶

Coq enters proof mode when you begin a proof through commands such as Theorem or Goal. Coq user interfaces usually have a way to indicate that you're in proof mode.

Tactics are available only in proof mode (currently they give syntax errors outside of proof mode). Most commands can be used both in and out of proof mode, but some commands only work in or outside of proof mode.

When the proof is completed, you can exit proof mode with commands such as Qed, Defined and Save.

Command Goal type¶: Asserts an unnamed proposition. This is intended for quick tests that a proposition is provable. If the proof is eventually completed and validated, you can assign a name with the Save or Defined commands. If no name is given, the name will be Unnamed_thm (or, if that name is already defined, a variant of that).

Command Qed¶

Passes a completed proof term to Coq's kernel to check that the proof term is well-typed and to verify that its type matches the theorem statement. If it's verified, the proof term is added to the global environment as an opaque constant using the declared name from the original goal.

It's very rare for a proof term to fail verification. Generally this indicates a bug in a tactic you used or that you misused some unsafe tactics.

Error Attempt to save an incomplete proof.¶

Error No focused proof (No proof-editing in progress).¶: You tried to use a proof mode command such as Qed outside of proof mode.

Note

Sometimes an error occurs when building the proof term, because tactics do not enforce completely the term construction constraints.

The user should also be aware of the fact that since the proof term is completely rechecked at this point, one may have to wait a while when the proof is large. In some exceptional cases one may even incur a memory overflow.

Command Save ident¶: Similar to Qed, except that the proof term is added to the global context with the name ident, which overrides any name provided by the Theorem command or its variants.

Command Defined ident?¶: Similar to Qed and Save, except the proof is made transparent, which means that its content can be explicitly used for type checking and that it can be unfolded in conversion tactics (see Applying conversion rules, Opaque, Transparent). If ident is specified, the proof is defined with the given name, which overrides any name provided by the Theorem command or its variants.

Command Admitted¶: This command is available in proof mode to give up the current proof and declare the initial goal as an axiom.

Command Abort All?¶

Aborts the current proof. If the current proof is a nested proof, the previous proof becomes current. If All is given, all nested proofs are aborted. See Nested Proofs Allowed.

All: Aborts all current proofs.

Error No focused proof (No proof-editing in progress).¶

Command Proof term¶: This command applies in proof mode. It is equivalent to exact term. Qed. That is, you have to give the full proof in one gulp, as a proof term (see Section Applying theorems).

Warning

Use of this command is discouraged. In particular, it doesn't work in Proof General because it must immediately follow the command that opened proof mode, but Proof General inserts Unset Silent before it (see Proof General issue #498).

Command Proof¶: Is a no-op which is useful to delimit the sequence of tactic commands which start a proof, after a Theorem command. It is a good practice to use Proof as an opening parenthesis, closed in the script with a closing Qed.

See also

Proof with

Command Proof using section_var_expr with ltac_expr?¶

Opens proof mode, declaring the set of section variables (see Assumptions) used by the proof. These proof annotations are useful to enable asynchronous processing of proofs. This example shows how they work. The Qed command verifies that the set of section variables used in the proof is a subset of the declared ones.

The set of declared variables is closed under type dependency. For example, if T is a variable and a is a variable of type T, then the commands Proof using a and Proof using T a are equivalent.

The set of declared variables always includes the variables used by the statement. In other words Proof using e is equivalent to Proof using Type + e for any declaration expression e.

- section_var_expr50: Use all section variables except those specified by section_var_expr50
section_var_expr0 + section_var_expr0: Use section variables from the union of both collections. See Name a set of section hypotheses for Proof using to see how to form a named collection.
section_var_expr0 - section_var_expr0: Use section variables which are in the first collection but not in the second one.
*?: Use the transitive closure of the specified collection.
Type: Use only section variables occurring in the statement. Specifying * uses the forward transitive closure of all the section variables occurring in the statement. For example, if the variable H has type p < 5 then H is in p* since p occurs in the type of H.
All: Use all section variables.

Warning ident is both name of a Collection and Variable, Collection ident takes precedence over Variable.¶: If a specified name is ambiguous (it could be either a Collection or a Variable), then it is assumed to be a Collection name.

Warning Variable All is shadowed by Collection named All containing all variables.¶: This is variant of the previous warning for the All collection.

Proof using options¶

The following options modify the behavior of Proof using.

Option Default Proof Using "section_var_expr"¶

Set this option to use section_var_expr as the default Proof using value. E.g. Set Default Proof Using "a b" will complete all Proof commands not followed by a using part with using a b.

Note that section_var_expr isn't validated immediately. An invalid value will generate an error on a subsequent Proof or Qed command.

Flag Suggest Proof Using¶: When this flag is on, Qed suggests a using annotation if the user did not provide one.

Name a set of section hypotheses for `Proof using`¶

Command Collection ident := section_var_expr¶

This can be used to name a set of section hypotheses, with the purpose of making Proof using annotations more compact.

Example

Define the collection named Some containing x, y and z:

Collection Some := x y z.

Define the collection named Fewer containing only x and y:

Collection Fewer := Some - z

Define the collection named Many containing the set union or set difference of Fewer and Some:

Collection Many := Fewer + Some
Collection Many := Fewer - Some

Define the collection named Many containing the set difference of Fewer and the unnamed collection x y:

Collection Many := Fewer - (x y)

Deprecated since version 8.15: Redefining a collection, defining a collection with the same name as a variable, and invoking the Proof using command when collection and variable names overlap are deprecated. See the warnings below and in the Proof using command.

Error "All" is a predefined collection containing all variables. It can't be redefined.¶: When issuing a Proof using command, All used as a collection name always means "use all variables".

Warning New Collection definition of ident shadows the previous one.¶: Redefining a Collection overwrites the previous definition.

Warning ident was already a defined Variable, the name ident will refer to Collection when executing "Proof using" command.¶: The Proof using command allows specifying both Collection and Variable names. In case of ambiguity, a name is assumed to be Collection name.

Proof modes¶

When entering proof mode through commands such as Goal and Proof, Coq picks by default the L_tac mode. Nonetheless, there exist other proof modes shipped in the standard Coq installation, and furthermore some plugins define their own proof modes. The default proof mode used when opening a proof can be changed using the following option.

Option Default Proof Mode string¶

This option selects the proof mode to use when starting a proof. Depending on the proof mode, various syntactic constructs are allowed when writing a proof. All proof modes support commands; the proof mode determines which tactic language and set of tactic definitions are available. The possible option values are:

"Classic": Activates the L_tac language and the tactics with the syntax documented in this manual. Some tactics are not available until the associated plugin is loaded, such as SSR or micromega. This proof mode is set when the prelude is loaded.
"Noedit": No tactic language is activated at all. This is the default when the prelude is not loaded, e.g. through the -noinit option for coqc.
"Ltac2": Activates the Ltac2 language and the Ltac2-specific variants of the documented tactics. This value is only available after Requiring Ltac2. Importing Ltac2 sets this mode.

Some external plugins also define their own proof mode, which can be activated with this command.

Command Proof Mode string¶: Sets the proof mode within the current proof.

Managing goals¶

Command Undo To? natural?¶: Cancels the effect of the last natural commands or tactics. The To natural form goes back to the specified state number. If natural is not specified, the command goes back one command or tactic.

Command Restart¶

Restores the proof to the original goal.

Error No focused proof to restart.¶

Focusing goals¶

Focusing lets you limit the context display to (initially) a single goal. If a tactic creates additional goals from a focused goal, the subgoals are also focused. The two focusing constructs are curly braces ({ and }) and bullets (e.g. -, + or *). These constructs can be nested.

Curly braces¶

Tactic natural[ ident ] :? {¶

Tactic }¶

{ (without a terminating period) focuses on the first goal. The subproof can only be unfocused when it has been fully solved (i.e., when there is no focused goal left). Unfocusing is then handled by } (again, without a terminating period). See also an example in the next section.

Note that when a focused goal is proved a message is displayed together with a suggestion about the right bullet or } to unfocus it or focus the next one.

natural:: Focuses on the natural-th goal to prove.

[ ident ]: {
Focuses on the goal named ident even if the goal is not in focus. Goals are existential variables, which don't have names by default. You can give a name to a goal by using refine ?[ident].

Example: Working with named goals

Ltac name_goal name := refine ?[name]. (* for convenience *)
name_goal is defined

Set Printing Goal Names. (* show goal names, e.g. "(?base)" and "(?step)" *)

Goal forall n, n + 0 = n.
1 goal (?Goal) ============================ forall n : nat, n + 0 = n

Proof.
induction n; [ name_goal base | name_goal step ].
2 goals, goal 1 (?base) ============================ 0 + 0 = 0 goal 2 (?step) is: S n + 0 = S n

(* focus on the goal named "base" *)
[base]: { reflexivity.
1 goal (?base) ============================ 0 + 0 = 0 This subproof is complete, but there are some unfocused goals. Try unfocusing with "}". 1 goal goal 1 (?step) is: S n + 0 = S n

}
1 goal (?step) n : nat IHn : n + 0 = n ============================ S n + 0 = S n

This can also be a way of focusing on a shelved goal, for instance:

Goal exists n : nat, n = n.
1 goal ============================ exists n : nat, n = n

eexists ?[x].
1 focused goal (shelved: 1) ============================ ?x = ?x

reflexivity.
All the remaining goals are on the shelf. 1 goal goal 1 is: nat

[x]: exact 0.
No more goals.

Qed.

Error This proof is focused, but cannot be unfocused this way.¶

You are trying to use } but the current subproof has not been fully solved.

Error No such goal (natural).¶

Error No such goal (ident).¶

Error Brackets do not support multi-goal selectors.¶

Brackets are used to focus on a single goal given either by its position or by its name if it has one.

See also

The error messages for bullets below.

Bullets¶

Alternatively, proofs can be structured with bullets instead of { and }. The first use of a bullet b focuses on the first goal g. The same bullet can't be used again until the proof of g is completed, then the next goal must be focused with another b. Thus, all the goals present just before the first use of the bullet must be focused with the same bullet b. See the example below.

Different bullets can be used to nest levels. The scope of each bullet is limited to the enclosing { and }, so bullets can be reused as further nesting levels provided they are delimited by curly braces. Bullets are made from -, + or * characters (with no spaces and no period afterward):

Tactic bullet¶: bullet::=-+++*+

When a focused goal is proved, Coq displays a message suggesting use of } or the correct matching bullet to unfocus the goal or focus the next subgoal.

Note

In Proof General (Emacs interface to Coq), you must use bullets with the priority ordering shown above to have correct indentation. For example - must be the outer bullet and + the inner one in the example below.

Example: Use of bullets

For the sake of brevity, the output for this example is summarized in comments. Note that the tactic following a bullet is frequently put on the same line with the bullet. Observe that this proof still works even if all the bullets in it are omitted.

Goal (1=1 /\ 2=2) /\ 3=3.: 1 goal ============================ (1 = 1 /\ 2 = 2) /\ 3 = 3
Proof.
split. (* 1 = 1 /\ 2 = 2 and 3 = 3 *): 2 goals ============================ 1 = 1 /\ 2 = 2 goal 2 is: 3 = 3
- (* 1 = 1 /\ 2 = 2 *): 1 goal ============================ 1 = 1 /\ 2 = 2
split. (* 1 = 1 and 2 = 2 *): 2 goals ============================ 1 = 1 goal 2 is: 2 = 2
+ (* 1 = 1 *): 1 goal ============================ 1 = 1
trivial. (* subproof complete *): This subproof is complete, but there are some unfocused goals. Focus next goal with bullet +. 2 goals goal 1 is: 2 = 2 goal 2 is: 3 = 3
+ (* 2 = 2 *): 1 goal ============================ 2 = 2
trivial. (* subproof complete *): This subproof is complete, but there are some unfocused goals. Focus next goal with bullet -. 1 goal goal 1 is: 3 = 3
- (* 3 = 3 *): 1 goal ============================ 3 = 3
trivial. (* No more subgoals *): No more goals.
Qed.

Error Wrong bullet bullet₁: Current bullet bullet₂ is not finished.¶: Before using bullet bullet₁ again, you should first finish proving the current focused goal. Note that bullet₁ and bullet₂ may be the same.

Error Wrong bullet bullet₁: Bullet bullet₂ is mandatory here.¶: You must put bullet₂ to focus on the next goal. No other bullet is allowed here.

Error No such goal. Focus next goal with bullet bullet.¶: You tried to apply a tactic but no goals were under focus. Using bullet is mandatory here.

Error No such goal. Try unfocusing with }.¶: You just finished a goal focused by {, you must unfocus it with }.

Note

Use Default Goal Selector with the ! selector to force the use of focusing mechanisms (bullets, braces) and goal selectors so that it is always explicit to which goal(s) a tactic is applied.

Option Bullet Behavior "None""Strict Subproofs"¶

This option controls the bullet behavior and can take two possible values:

"None": this makes bullets inactive.
"Strict Subproofs": this makes bullets active (this is the default behavior).

Other focusing commands¶

Command Unfocused¶: Succeeds if there are no unfocused goals. Otherwise the command fails.

Command Focus natural?¶: Focuses the attention on the first goal to prove or, if natural is specified, the natural-th. The printing of the other goals is suspended until the focused goal is solved or unfocused.

Deprecated since version 8.8: Prefer the use of bullets or focusing braces with a goal selector (see above).

Command Unfocus¶: Restores to focus the goals that were suspended by the last Focus command.

Deprecated since version 8.8.

Shelving goals¶

Goals can be shelved so they are no longer displayed in the proof state. Shelved goals can be unshelved with the Unshelve command, which makes all shelved goals visible in the proof state. You can use the goal selector [ ident ]: { to focus on a single shelved goal (see here). Currently there's no single command or tactic that unshelves goals by name.

Tactic shelve¶: Moves the focused goals to the shelf. They will no longer be displayed in the context. The Show Existentials command will still show these goals, which will be marked "(shelved)".

Tactic shelve_unifiable¶

Shelves only the goals under focus that are mentioned in other goals. Goals that appear in the type of other goals can be solved by unification.

Example: shelve_unifiable

Goal exists n, n=0.: 1 goal ============================ exists n : nat, n = 0
refine (ex_intro _ _ _).: 1 focused goal (shelved: 1) ============================ ?Goal = 0
all: shelve_unifiable.
reflexivity.: No more goals.

Command Unshelve¶: This command moves all the goals on the shelf (see shelve) from the shelf into focus, by appending them to the end of the current list of focused goals.

Tactic unshelve ltac_expr1¶: Performs tactic, then unshelves existential variables added to the shelf by the execution of tactic, prepending them to the current goal.

Tactic admit¶
Tactic give_up¶: Allows skipping a subgoal to permit further progress on the rest of the proof. The selected goals are removed from the context. They are not solved and cannot be solved later in the proof. Since the goals are not solved, the proof cannot be closed with Qed but only with Admitted.

Reordering goals¶

Tactic cycle int_or_var¶

Reorders the selected goals so that the first integer goals appear after the other selected goals. If integer is negative, it puts the last integer goals at the beginning of the list. The tactic is only useful with a goal selector, most commonly all:. Note that other selectors reorder goals; 1,3: cycle 1 is not equivalent to all: cycle 1. See … : … (goal selector).

Example: cycle

Parameter P : nat -> Prop.: P is declared

Goal P 1 /\ P 2 /\ P 3 /\ P 4 /\ P 5.: 1 goal ============================ P 1 /\ P 2 /\ P 3 /\ P 4 /\ P 5
repeat split. (* P 1, P 2, P 3, P 4, P 5 *): 5 goals ============================ P 1 goal 2 is: P 2 goal 3 is: P 3 goal 4 is: P 4 goal 5 is: P 5
all: cycle 2. (* P 3, P 4, P 5, P 1, P 2 *): 5 goals ============================ P 3 goal 2 is: P 4 goal 3 is: P 5 goal 4 is: P 1 goal 5 is: P 2
all: cycle -3. (* P 5, P 1, P 2, P 3, P 4 *): 5 goals ============================ P 5 goal 2 is: P 1 goal 3 is: P 2 goal 4 is: P 3 goal 5 is: P 4

Tactic swap int_or_var int_or_var¶

Exchanges the position of the specified goals. Negative values for integer indicate counting goals backward from the end of the list of selected goals. Goals are indexed from 1. The tactic is only useful with a goal selector, most commonly all:. Note that other selectors reorder goals; 1,3: swap 1 3 is not equivalent to all: swap 1 3. See … : … (goal selector).

Example: swap

Goal P 1 /\ P 2 /\ P 3 /\ P 4 /\ P 5.: 1 goal ============================ P 1 /\ P 2 /\ P 3 /\ P 4 /\ P 5
repeat split. (* P 1, P 2, P 3, P 4, P 5 *): 5 goals ============================ P 1 goal 2 is: P 2 goal 3 is: P 3 goal 4 is: P 4 goal 5 is: P 5
all: swap 1 3. (* P 3, P 2, P 1, P 4, P 5 *): 5 goals ============================ P 3 goal 2 is: P 2 goal 3 is: P 1 goal 4 is: P 4 goal 5 is: P 5
all: swap 1 -1. (* P 5, P 2, P 1, P 4, P 3 *): 5 goals ============================ P 5 goal 2 is: P 2 goal 3 is: P 1 goal 4 is: P 4 goal 5 is: P 3

Tactic revgoals¶

Reverses the order of the selected goals. The tactic is only useful with a goal selector, most commonly all :. Note that other selectors reorder goals; 1,3: revgoals is not equivalent to all: revgoals. See … : … (goal selector).

Example: revgoals

Goal P 1 /\ P 2 /\ P 3 /\ P 4 /\ P 5.: 1 goal ============================ P 1 /\ P 2 /\ P 3 /\ P 4 /\ P 5
repeat split. (* P 1, P 2, P 3, P 4, P 5 *): 5 goals ============================ P 1 goal 2 is: P 2 goal 3 is: P 3 goal 4 is: P 4 goal 5 is: P 5
all: revgoals. (* P 5, P 4, P 3, P 2, P 1 *): 5 goals ============================ P 5 goal 2 is: P 4 goal 3 is: P 3 goal 4 is: P 2 goal 5 is: P 1

Proving a subgoal as a separate lemma: abstract¶

Tactic abstract ltac_expr2 using ident_name?¶

Does a solve [ ltac_expr2 ] and saves the subproof as an auxiliary lemma. if ident_name is specified, the lemma is saved with that name; otherwise the lemma is saved with the name ident_subproofnatural? where ident is the name of the current goal (e.g. the theorem name) and natural is chosen to get a fresh name. If the proof is closed with Qed, the auxiliary lemma is inlined in the final proof term.

This is useful with tactics such as discriminate that generate huge proof terms with many intermediate goals. It can significantly reduce peak memory use. In most cases it doesn't have a significant impact on run time. One case in which it can reduce run time is when a tactic foo is known to always pass type checking when it succeeds, such as in reflective proofs. In this case, the idiom "abstract exact_no_check foo" will save half the type checking type time compared to "exact foo".

abstract is an l3_tactic.

Warning

The abstract tactic, while very useful, still has some known limitations. See #9146 for more details. We recommend caution when using it in some "non-standard" contexts. In particular, abstract doesn't work properly when used inside quotations ltac:(...). If used as part of typeclass resolution, it may produce incorrect terms when in polymorphic universe mode.

Warning

Provide ident_name at your own risk; explicitly named and reused subterms don’t play well with asynchronous proofs.

Tactic transparent_abstract ltac_expr3 using ident?¶

Like abstract, but save the subproof in a transparent lemma with a name in the form ident_subtermnatural?.

Warning

Use this feature at your own risk; building computationally relevant terms with tactics is fragile, and explicitly named and reused subterms don’t play well with asynchronous proofs.

Error Proof is not complete.¶

Requesting information¶

Command Show identnatural?¶

Displays the current goals.

natural

Display only the natural-th goal.

ident

Displays the named goal ident. This is useful in particular to display a shelved goal but only works if the corresponding existential variable has been named by the user (see Existential variables) as in the following example.

Example

Goal exists n, n = 0.: 1 goal ============================ exists n : nat, n = 0
eexists ?[n].: 1 focused goal (shelved: 1) ============================ ?n = 0
Show n.: goal n is: ============================ nat

Error No focused proof.¶

Error No such goal.¶

Command Show Proof Diffs removed??¶

Displays the proof term generated by the tactics that have been applied so far. If the proof is incomplete, the term will contain holes, which correspond to subterms which are still to be constructed. Each hole is an existential variable, which appears as a question mark followed by an identifier.

Specifying “Diffs” highlights the difference between the current and previous proof step. By default, the command shows the output once with additions highlighted. Including “removed” shows the output twice: once showing removals and once showing additions. It does not examine the Diffs option. See "Show Proof" differences.

Command Show Conjectures¶: Prints the names of all the theorems that are currently being proved. As it is possible to start proving a previous lemma during the proof of a theorem, there may be multiple names.

Command Show Intro¶: If the current goal begins by at least one product, prints the name of the first product as it would be generated by an anonymous intro. The aim of this command is to ease the writing of more robust scripts. For example, with an appropriate Proof General macro, it is possible to transform any anonymous intro into a qualified one such as intro y13. In the case of a non-product goal, it prints nothing.

Command Show Intros¶: Similar to the previous command. Simulates the naming process of intros.

Command Show Existentials¶: Displays all open goals / existential variables in the current proof along with the context and type of each variable.

Command Show Match qualid¶

Displays a template of the Gallina match construct with a branch for each constructor of the type qualid. This is used internally by company-coq.

Example

Show Match nat.: match # with | O => | S x => end

Error Unknown inductive type.¶

Command Show Universes¶: Displays the set of all universe constraints and its normalized form at the current stage of the proof, useful for debugging universe inconsistencies.

Command Show Goal natural at natural¶: Available in coqtop. Displays a goal at a proof state using the goal ID number and the proof state ID number. It is primarily for use by tools such as Prooftree that need to fetch goal history in this way. Prooftree is a tool for visualizing a proof as a tree that runs in Proof General.

Command Guarded¶

Some tactics (e.g. refine) allow to build proofs using fixpoint or cofixpoint constructions. Due to the incremental nature of proof construction, the check of the termination (or guardedness) of the recursive calls in the fixpoint or cofixpoint constructions is postponed to the time of the completion of the proof.

The command Guarded allows checking if the guard condition for fixpoint and cofixpoint is violated at some time of the construction of the proof without having to wait the completion of the proof.

Showing differences between proof steps¶

Coq can automatically highlight the differences between successive proof steps and between values in some error messages. Coq can also highlight differences in the proof term. For example, the following screenshots of CoqIDE and coqtop show the application of the same intros tactic. The tactic creates two new hypotheses, highlighted in green. The conclusion is entirely in pale green because although it’s changed, no tokens were added to it. The second screenshot uses the "removed" option, so it shows the conclusion a second time with the old text, with deletions marked in red. Also, since the hypotheses are new, no line of old text is shown for them.

This image shows an error message with diff highlighting in CoqIDE:

How to enable diffs¶

Option Diffs "on""off""removed"¶: This option is used to enable diffs. The “on” setting highlights added tokens in green, while the “removed” setting additionally reprints items with removed tokens in red. Unchanged tokens in modified items are shown with pale green or red. Diffs in error messages use red and green for the compared values; they appear regardless of the setting. (Colors are user-configurable.)

For coqtop, showing diffs can be enabled when starting coqtop with the -diffs on|off|removed command-line option or by setting the Diffs option within Coq. You will need to provide the -color on|auto command-line option when you start coqtop in either case.

Colors for coqtop can be configured by setting the COQ_COLORS environment variable. See section Environment variables. Diffs use the tags diff.added, diff.added.bg, diff.removed and diff.removed.bg.

In CoqIDE, diffs should be enabled from the View menu. Don’t use the Set Diffs command in CoqIDE. You can change the background colors shown for diffs from the Edit | Preferences | Tags panel by changing the settings for the diff.added, diff.added.bg, diff.removed and diff.removed.bg tags. This panel also lets you control other attributes of the highlights, such as the foreground color, bold, italic, underline and strikeout.

Proof General, VsCoq and Coqtail can also display Coq-generated proof diffs automatically. Please see the PG documentation section "Showing Proof Diffs" and Coqtail's "Proof Diffs" for details.

How diffs are calculated¶

Diffs are calculated as follows:

Select the old proof state to compare to, which is the proof state before the last tactic that changed the proof. Changes that only affect the view of the proof, such as all: swap 1 2, are ignored.
For each goal in the new proof state, determine what old goal to compare it to—the one it is derived from or is the same as. Match the hypotheses by name (order is ignored), handling compacted items specially.
For each hypothesis and conclusion (the “items”) in each goal, pass them as strings to the lexer to break them into tokens. Then apply the Myers diff algorithm [Mye86] on the tokens and add appropriate highlighting.

Notes:

Aside from the highlights, output for the "on" option should be identical to the undiffed output.
Goals completed in the last proof step will not be shown even with the "removed" setting.

This screenshot shows the result of applying a split tactic that replaces one goal with 2 goals. Notice that the goal P 1 is not highlighted at all after the split because it has not changed.

Diffs may appear like this after applying a intro tactic that results in a compacted hypotheses:

"Show Proof" differences¶

To show differences in the proof term:

In coqtop and Proof General, use the Show Proof Diffs command.
In CoqIDE, position the cursor on or just after a tactic to compare the proof term after the tactic with the proof term before the tactic, then select View / Show Proof from the menu or enter the associated key binding. Differences will be shown applying the current Show Diffs setting from the View menu. If the current setting is Don't show diffs, diffs will not be shown.

Output with the "added and removed" option looks like this:

Delaying solving unification constraints¶

Tactic solve_constraints¶

Flag Solve Unification Constraints¶: By default, after each tactic application, postponed typechecking unification problems are resolved using heuristics. Unsetting this flag disables this behavior, allowing tactics to leave unification constraints unsolved. Use the solve_constraints tactic at any point to solve the constraints.

Proof maintenance¶

Experimental. Many tactics, such as intros, can automatically generate names, such as "H0" or "H1" for a new hypothesis introduced from a goal. Subsequent proof steps may explicitly refer to these names. However, future versions of Coq may not assign names exactly the same way, which could cause the proof to fail because the new names don't match the explicit references in the proof.

The following Mangle Names settings let users find all the places where proofs rely on automatically generated names, which can then be named explicitly to avoid any incompatibility. These settings cause Coq to generate different names, producing errors for references to automatically generated names.

Flag Mangle Names¶: When this flag is set (it is off by default), generated names use the prefix specified in the following option instead of the default prefix.

Option Mangle Names Prefix string¶: This option specifies the prefix to use when generating names.

Flag Mangle Names Light¶: When this flag is set (it is off by default), the names generated by Mangle Names only add the Mangle Names Prefix to the original name.

Controlling proof mode¶

Option Hyps Limit natural¶: This option controls the maximum number of hypotheses displayed in goals after the application of a tactic. All the hypotheses remain usable in the proof development. When unset, it goes back to the default mode which is to print all available hypotheses.

Flag Nested Proofs Allowed¶: When turned on (it is off by default), this flag enables support for nested proofs: a new assertion command can be inserted before the current proof is finished, in which case Coq will temporarily switch to the proof of this nested lemma. When the proof of the nested lemma is finished (with Qed or Defined), its statement will be made available (as if it had been proved before starting the previous proof) and Coq will switch back to the proof of the previous assertion.

Flag Printing Goal Names¶: When this flag is turned on, the name of the goal is printed in proof mode, which can be useful in cases of cross references between goals.

Flag Printing Goal Tags¶: Internal flag used to implement Proof General's proof-tree mode.

Controlling memory usage¶

Command Print Debug GC¶: Prints heap usage statistics, which are values from the stat type of the Gc module described here in the OCaml documentation. The live_words, heap_words and top_heap_words values give the basic information. Words are 8 bytes or 4 bytes, respectively, for 64- and 32-bit executables.

When experiencing high memory usage the following commands can be used to force Coq to optimize some of its internal data structures.

Command Optimize Proof¶: Shrink the data structure used to represent the current proof.

Command Optimize Heap¶: Perform a heap compaction. This is generally an expensive operation. See: OCaml Gc.compact There is also an analogous tactic optimize_heap.

Memory usage parameters can be set through the OCAMLRUNPARAM environment variable.

Proof mode¶

Proof State¶

Entering and exiting proof mode¶

Proof using options¶

Name a set of section hypotheses for Proof using¶

Proof modes¶

Managing goals¶

Focusing goals¶

Curly braces¶

Bullets¶

Other focusing commands¶

Shelving goals¶

Reordering goals¶

Proving a subgoal as a separate lemma: abstract¶

Requesting information¶

Showing differences between proof steps¶

How to enable diffs¶

How diffs are calculated¶

"Show Proof" differences¶

Delaying solving unification constraints¶

Proof maintenance¶

Controlling proof mode¶

Controlling memory usage¶

Name a set of section hypotheses for `Proof using`¶